4.9.8 La teoría de Galois

La teoría de Galois parte de un polinomio irreducible 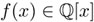, es decir, de un polinomio que no se puede factorizar como g(x) · h(x), donde  g(x) y h(x) son polinomios no constantes en 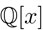. Se denota con K el campo de descomposición de f(x), es decir, el campo K  más pequeño que contiene .

La teoría de Galois establece una relación entre dos conjuntos. Por un lado, están los subgrupos de 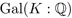, es decir, los subconjuntos de 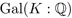que son cerrados bajo la multiplicación y la formación de inversos —y que siempre contienen la identidad como elemento—. Por otro, están los campos L intermedios, es decir, los campos L que satisfacen  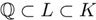. La correspondencia se da por dos funciones r y s:

Es decir, r asigna a cada subgrupo de 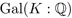un campo intermedio e, inversamente, la función asigna a cada campo intermedio uno de estos subgrupos. La función r se define por:

es decir, r (H)es el conjunto de números  z ∈ K  que permanecen fijos bajo cualquier φ de H. Por otro lado, se define que:

es decir, s(L)  es el conjunto de automorfismos 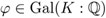tal que cualquier z ∈ L permanece fijo bajo φ . No es difícil ver que r y s son funciones inversas una de la otra.

Las contenciones se invierten bajo r y s: si  H ⊂   H´son subgrupos de 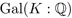, entonces  r(H) ⊃ r(H´) y viceversa, si L ⊂ L´ son dos campos intermedios, entonces s (L´) ⊃ s (L´)  . Al subgrupo H = {id}, que contiene solamente la identidad y que es el subgrupo más pequeño, corresponde el campo intermedio más grande, que es  K mismo, mientras que al subgrupo más grande, que es , corresponde el campo intermedio más pequeño, que es .

Así, en el caso del polinomio f(x)= x⁴ + 1 se ve que los cálculos anteriores ejemplifican la teoría de Galois, como se ve en la figura 4.58.

Figura 4.60 Del lado izquierdo, la correspondencia entre subgrupos del grupo de Galois, y del derecho los {id} campos intermedios.

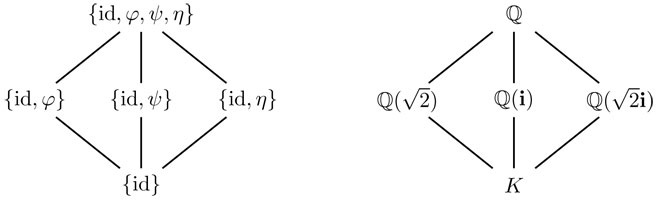
Se puede mostrar que el polinomio f(x)= x⁵  + x + 1 es irreducible con cinco raíces distintas  s₁, …, s₅ y el grupo de Galois 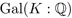es todo el grupo de permutaciones de las cinco raíces s₁, …, s₅. En general, para cada n es posible encontrar un polinomio irreducible  de grado n tal que el grupo 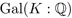es todo el grupo de permutaciones de las raíces n distintas.

Por ello, es importante estudiar los subgrupos del grupo de permutaciones de n elementos distintos s₁, …, s_n. Dicho estudio es el inicio de la teoría de grupos que se estudian por sí mismos desde entonces, sin conexión con el origen de la resolución de ecuaciones. El grupo de permutaciones tiene una estructura que no depende de cuáles sean los n elementos a permutar. Por consiguiente, las podemos elegir como los números  1, 2, …., n para facilitar la notación.  El grupo resultante se denota por  S_n y se llama grupo simétrico. A continuación, resumimos algunos de los hechos de la teoría de grupos que serán de relevancia en lo que sigue.

Una transposición es una permutación que deja fijos todos los elementos, salvo dos que intercambia. Si  i y j son los dos elementos intercambiados, la transposición se denota por (i j). Cada permutación se puede escribir como composición de transposiciones. El número de transposiciones usadas en una composición no es invariante, por ejemplo, se tiene que:

(12)(23)(12) = 13

Sin embargo, la paridad del número de transposiciones usadas sí es una invariante: una composición de 3 transposiciones no se puede escribir como composición de un número par de transposiciones. Por ello, el conjunto de composiciones A_n de un númeropar de transposiciones forma un subgrupo, llamado el grupo alternante.

 El subgrupo A_n es un subgrupo normal de Sn, es decir, para cada α ∈ A_n y cada σ ∈ S_n  se tiene σ-¹ασ ∈ A_n . Si n = 4, entonces A₄ tiene un subgrupo normal, a la vez, que es el subgrupo de Klein:

K = {Id, (12)(34), (13)(24), (14)(23)}

Éste es justamente el grupo de Galois 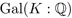  si  K es el campo de descomposición del polinomio f (x)= x⁴  + 1 , el ejemplo que hemos seguido más de cerca hasta ahora.

Aquí se debe tener cuidado: es subgrupo no normal de S₄ pero sí es normal en A₄. El grupo K tiene, a la vez, tres subgrupos normales:  Z₁ = {Id, (12)(34)},  Z₂=  {Id, (13)(24)}  y Z₃ =  {Id, (14)(23)}. Si H es subgrupo normal de H´, se denota por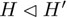. Con ello tenemos la siguiente sucesión de subgrupos normales:

Ésta es una sucesión de composición de  S4 donde ya no es posible insertar más subgrupos en medio sin tener igualdad. Si escribimos la cardinalidad en lugar de los grupos, obtenemos la siguiente sucesión de divisores 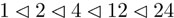. Los factores entre dos números sucesivos son primos.

En la teoría de grupos es posible formar cocientes de subgrupos si éstos son normales y, además, la cardinalidad de estos grupos cocientes es justo el factor de los números consecutivos correspondientes. Más aún, cualquier grupo con un número primo de elementos es conmutativo. Los grupos conmutativos se llaman también abelianos, en honor a Abel, quien enfatizó la importancia de este hecho para la resolución de las ecuaciones.

Las siguientes cadenas muestran sucesiones de composición de S₂ y S₃:

Las cardinalidades 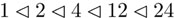son y, respectivamente. En consecuencia, S₂S₃ y S₄ tienen sucesiones de composición con factores abelianos. También  S₅ y, más general, S_n para n ≥ 5 tiene una sucesión de composición:

pero A_n no es conmutativo. Los únicos subgrupos normales de A_n son {Id} y A_n . Es fácil ver que, A_n para n ≥  5, no es conmutativo. La importancia de esta diferencia reside en lo que se explica a continuación.

La teoría de Galois establece una muy buena correspondencia entre los subgrupos de 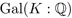 y los campos intermedios 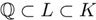: el subgrupo H ⊂H' es normal en H' si y solamente si L = r(H) es una extensión normal de L' = r(H), es decir, cada g(x)∈ L´ [x] que tiene una raíz en L, tiene todas las raíces en L. Además, en este caso podemos considerar el cociente H´ / H. Este cociente es cíclico —es decir, es isomorfo al grupo dado por {1,…, n} bajo la adición módulo n— si  y solamente si L es una extensión cíclica de L', es decir existe un elemento a ∈ L´ tal que L es el campo de descomposición del polinomio xⁿ - a ∈ L´ [x] . En otras palabras, todos los elementos de L se pueden escribir como combinaciones de 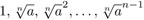con coeficientes en L.¹

Si se junta toda esta información, se obtiene que el hecho de que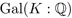tiene una sucesión de composición con factores abelianos corresponde a que las soluciones de la ecuación f(x) = 0 se pueden escribir con números racionales, las cuatro operaciones básicas y raíces. El grupo S_n no es soluble, es decir, no tiene una sucesión de composición con factores abelianos. Consecuentemente, un polinomio f(x) cuyo grupo de Galois  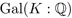es isomorfo a S_n, no será soluble por radicales, lo cual significa que sus raíces no se podrán escribir usando los coeficientes, las operaciones básicas y raíces cuadradas. Como hemos visto, hay siempre polinomios con esa propiedad. Así se establece una visión más profunda de la imposibilidad de poder dar una fórmula de solución para las ecuaciones algebraicas de grado mayor que 4.

Es una coincidencia triste que, tanto Abel como Galois, murieran a temprana edad. Niels Henrik Abel nació en Noruega en 1802, pero era muy pobre y sólo gracias a una beca pudo viajar a Europa para presentar sus brillantes ideas en los centros de investigación matemática. Viajó a Berlín y luego a París, pero no obtuvo una recepción favorable ni logró despertar el interés de los líderes matemáticos de aquel tiempo, como Gauss, Legendre o Cauchy. En París contrajo tuberculosis y murió a la edad de 27 años, dos días antes de que llegara la carta de Berlín que le informaba que había conseguido un puesto de profesor.

Figura 4.61 Sello conmemorativo por los 100 años de la muerte de Evariste Galois (1811-1832), matemático francés que murió con tan sólo 20 años en un duelo. Años más tarde, otro matemático alemán —Felix Klein— diría: "En Francia apareció hacia 1800 una nueva estrella de inimaginable brillo en el firmamento de las matemáticas: Evariste Galois".

Galois nació en 1811, en Francia, y murió a los 20 años en un duelo en el que había retado a un oficial, por motivos desconocidos. Vivió en tiempos turbios y difíciles. Lo que se sabe de su corta vida habla de que era una persona rebelde. Fue expulsado de la escuela, estuvo en prisión y lideró protestas. La noche anterior al duelo, escribió una última carta donde reportó y resumió frenéticamente sus ideas matemáticas, a sabiendas de que la muerte lo esperaba al principio del día siguiente. A Galois debemos la idea de considerar varias permutaciones de las raíces a la vez y, con ello, toda la teoría de grupos.

Hemos recorrido un camino largo y sinuoso. Primero, necesitábamos delimitar la pregunta y llegamos a la noción de ecuaciones algebraicas. Expandimos la noción de los números reales a los números complejos para poder resolver cualquier ecuación cuadrática. Después, consideramos la ecuación de tercer grado y vimos que, por el teorema fundamental del álgebra, la ecuación algebraica de cualquier grado positivo siempre tiene soluciones. El problema consiste en encontrar una fórmula para las soluciones a partir de los coeficientes que aparecen en la ecuación. Finalmente, descubrimos que tal fórmula no existe por el teorema de Abel-Ruffini y que la teoría de Galois aporta una explicación profunda de este hecho. Esta teoría requiere de considerable abstracción pero es, indudablemente, una de las joyas del álgebra. Así concluimos el resumen sobre una de las cuatro preguntas fundamentales que consideraremos en este capítulo.

---